3.1 Areas
1. Si f(x)>0 en el intervalo [a,b] , el área =Según lo anterior para calcular el área comprendida entre una curva y = f(x) y el eje OX y las rectas x=a, x=b se procede así:
| |||
| |||
EJEMPLOS:
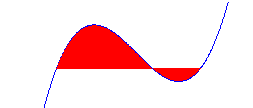
Hallar e área de la región limitada por las gráficas de y =x2 +2, y = -x, x =0 y x = 1.
Solución: Hacemos g(x) =-x y f(x) =x2+2, entonces g(x) " f(x) para todo x en [0, 1], como muestra la figura. Por tanto, el área del rectángulo representativo es
A = [f(x) - g(x)] x
= [(x2+ 2) - (-x)] x
A = 
[f(x) - g(x)] dx
[f(x) - g(x)] dx
= [(x2 + 2) - (-x)]dx
= [x3/3 + x2/2 + 2x]10
= 1/3 + ½ + 2 = 
Las gráficas de f(x) =x2+2 y g(x) = -x no se cortan, y los valores de a y b están dados explícitamente. Un tipo de problema más común involucra el área de una región limitada por dos gráficas que se interceptan, debiendo por tanto calcularse los valores de a y b.
Aplicación
El consumo total de gasolina para el transporte en los Estados Unidos desde 1960 hasta 1979 sigue un modelo de crecimiento descrito por la ecuación:
f(t) =0,000433t2 + 0,0962t + 2,76; -10 " t " 9
Donde se mide f(t) en miles de millones de barriles y en t en años, correspondiendo t = 0 al primero de enero de 1970. Debido al aumento drástico de los precios del crudo a finales de los años setenta, el modelo de crecimiento del consumo cambió y comenzó a seguir esta otra forma:
g(t) = -0,00831t2 + 0,152t + 2,81; 9 " t " 16
Como muestra la siguiente figura. Calcular la cantidad total de gasolina ahorrada desde 1979 hasta 1985 como resultado de este cambio en los modelos que expresan estos ritmos de consumo.
Solución: Al estar situada la gráfica del modelo que regía hasta 1979 por encima de la del modelo posterior en el intervalo [9, 16] la cantidad de gasolina ahorrada viene dada por la integral siguiente:
f(t) g(t)
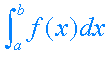
No hay comentarios:
Publicar un comentario