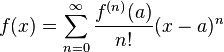Por medio de la presente informo que el equipo obtuvo el 100%
Atentamente
Ing.Enrique Marquez.
viernes, 27 de mayo de 2011
4.6 serie de taylor
inferior en una unidad, y las derivadas de orden n+1 y superiores de un polinomio de grado n son nulas.
Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), ex, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático. Examinemos uno de estos métodos.
Fórmula de Taylor
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:
f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio si se conocen los valores de f(a) y de sus n primeras derivadas.
Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)n. Además, es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)n.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.
Si a los polinomios añadimos las funciones de la forma y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos esencialmente las funciones cuyos valores pueden calcularse por métodos aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras funciones tales como log(x), sen(x), ex, ..., pero, aunque se estudian sus propiedades más importantes, no se da una respuesta a las preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a estas preguntas la proporcionan los métodos desarrollados por el análisis matemático. Examinemos uno de estos métodos.
Fórmula de Taylor
Sea f(x) una función definida en un intervalo que contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) + f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y también, como se comprueba fácilmente, la misma derivada que f(x) en este punto. Su gráfica es una recta tangente a la gráfica de f(x) en el punto a.
Es posible elegir un polinomio de segundo grado, p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2, tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la de f(x) más que la anterior. Es natural esperar que si construimos un polinomio que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto, este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así obtenemos la siguiente igualdad aproximada, que es la fórmula de Taylor:
f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a) (x-a)2 + ...... + (1/n!) f (n)(a) (x-a) n
El segundo miembro de esta fórmula es un polinomio de grado n en (x-a). Para cada valor de x puede calcularse el valor de este polinomio si se conocen los valores de f(a) y de sus n primeras derivadas.
Para funciones que tienen derivada (n+1)-ésima, el segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del primero en una pequeña cantidad que tiende a cero más rápidamente que (x-a)n. Además, es el único polinomio de grado n que difiere de f(x), para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más rápidamente que (x-a)n.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior, debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+ ...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!) f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c convenientemente elegido, desconocido, pero interior al intervalo de extremos a y x.
La demostración de la igualdad anterior es bastante engorrosa, aunque sencilla en esencia.
miércoles, 25 de mayo de 2011
°°Representación de funciones por serie de Taylor°°
en este tema se mostrará cómo obtener representaciones en series de potencias de funciones que tienen derivadas de todos los órdenes, es decir, funciones que son infinitamente diferenciables. esta serie se denomina serie de Taylor de f en a
esta serie se denomina serie de Taylor de f en a
Aplicaciones
Además de la obvia aplicación de utilizar funciones polinómicas en lugar de funciones de mayor complejidad para analizar el comportamiento local de una función, las series de Taylor tienen muchas otras aplicaciones.Algunas de ellas son: análisis de límites y estudios paramétricos de los mismos, estimación de números irracionales acotando su error, teorema de L'Hopital para la resolución de límites indeterminados, estudio de puntos estacionarios en funciones (máximos o mínimos relativos o puntos sillas de tendencia estrictamente creciente o decreciente), estimación de integrales, determinación de convergencia y suma de algunas series importantes, estudio de orden y parámetro principal de infinitésimos, etc.
FUENTES:
°°Cálculo de integrales expresadas como serie de Taylor°°
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
FUENTES :
http://es.wikipedia.org/wiki/Serie_de_Taylor
sábado, 21 de mayo de 2011
°° BIENVENIDOS°°
Bienvenidos:
En este Blog podrás encontrar, Todos los temas relacionados al calculo integral; Encontrarás contenido teorico y videos de apoyo para facilitar el entendimiento.
Recuerda dejar tus comentarios y sugerencias, siempre son de gran ayuda.
En este Blog podrás encontrar, Todos los temas relacionados al calculo integral; Encontrarás contenido teorico y videos de apoyo para facilitar el entendimiento.
Recuerda dejar tus comentarios y sugerencias, siempre son de gran ayuda.
Suscribirse a:
Entradas (Atom)